Edit this page
Open and issue
Linear Regression¶
The linear regression (LR) model is a simple machine learning approach used for target variables that are continuous (i.e. variables that are real-valued). The LR model takes as its input both a vector of features (conventionally labeled X) and a vector of labels (y). Often different terminology is used —calling X our set of variables or predictors, and y our outcome or dependent variable—but the idea is the same. The data are plotted, and a straight line is then fit to these data points. The objective is to fit the line to the data points so that the distance between the line and points are minimized.
Let's return to our running house price-prediction example. Predicting sales price from the features is a regression problem, because sale price varies continuously. What we're trying to find is some optimal function that, given a matrix of feature scores, can produce a set of continuous values that best approximates (for whatever definition of "best" we like) the true house price of our houses.
First we import the required libraries then investigate the data:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
all_data = pd.read_csv('../data/house_prices.csv', sep=',', index_col=0).reset_index(drop=True)
all_data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1460 entries, 0 to 1459
Data columns (total 80 columns):
MSSubClass 1460 non-null int64
MSZoning 1460 non-null object
LotFrontage 1201 non-null float64
LotArea 1460 non-null int64
Street 1460 non-null object
Alley 91 non-null object
LotShape 1460 non-null object
LandContour 1460 non-null object
Utilities 1460 non-null object
LotConfig 1460 non-null object
LandSlope 1460 non-null object
Neighborhood 1460 non-null object
Condition1 1460 non-null object
Condition2 1460 non-null object
BldgType 1460 non-null object
HouseStyle 1460 non-null object
OverallQual 1460 non-null int64
OverallCond 1460 non-null int64
YearBuilt 1460 non-null int64
YearRemodAdd 1460 non-null int64
RoofStyle 1460 non-null object
RoofMatl 1460 non-null object
Exterior1st 1460 non-null object
Exterior2nd 1460 non-null object
MasVnrType 1452 non-null object
MasVnrArea 1452 non-null float64
ExterQual 1460 non-null object
ExterCond 1460 non-null object
Foundation 1460 non-null object
BsmtQual 1423 non-null object
BsmtCond 1423 non-null object
BsmtExposure 1422 non-null object
BsmtFinType1 1423 non-null object
BsmtFinSF1 1460 non-null int64
BsmtFinType2 1422 non-null object
BsmtFinSF2 1460 non-null int64
BsmtUnfSF 1460 non-null int64
TotalBsmtSF 1460 non-null int64
Heating 1460 non-null object
HeatingQC 1460 non-null object
CentralAir 1460 non-null object
Electrical 1459 non-null object
1stFlrSF 1460 non-null int64
2ndFlrSF 1460 non-null int64
LowQualFinSF 1460 non-null int64
GrLivArea 1460 non-null int64
BsmtFullBath 1460 non-null int64
BsmtHalfBath 1460 non-null int64
FullBath 1460 non-null int64
HalfBath 1460 non-null int64
BedroomAbvGr 1460 non-null int64
KitchenAbvGr 1460 non-null int64
KitchenQual 1460 non-null object
TotRmsAbvGrd 1460 non-null int64
Functional 1460 non-null object
Fireplaces 1460 non-null int64
FireplaceQu 770 non-null object
GarageType 1379 non-null object
GarageYrBlt 1379 non-null float64
GarageFinish 1379 non-null object
GarageCars 1460 non-null int64
GarageArea 1460 non-null int64
GarageQual 1379 non-null object
GarageCond 1379 non-null object
PavedDrive 1460 non-null object
WoodDeckSF 1460 non-null int64
OpenPorchSF 1460 non-null int64
EnclosedPorch 1460 non-null int64
3SsnPorch 1460 non-null int64
ScreenPorch 1460 non-null int64
PoolArea 1460 non-null int64
PoolQC 7 non-null object
Fence 281 non-null object
MiscFeature 54 non-null object
MiscVal 1460 non-null int64
MoSold 1460 non-null int64
YrSold 1460 non-null int64
SaleType 1460 non-null object
SaleCondition 1460 non-null object
SalePrice 1460 non-null int64
dtypes: float64(3), int64(34), object(43)
memory usage: 912.6+ KB
# Select only columns that are numeric
all_data = all_data.select_dtypes(['number'])
# Remove any rows that contain NaN
for ifeature in list(all_data):
all_data = all_data[pd.notnull(all_data[ifeature])]
all_data.shape
(1121, 37)
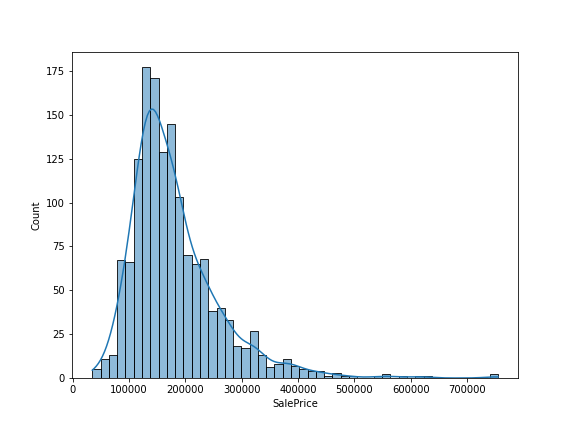
Let's also plot our target variable, Sales Price, to see what the distribution looks like:
sns.histplot(all_data['SalePrice'], kde=True)
Training a Linear Regression Model¶
We will need to first split up our data into an X array that contains the features to train on, and a y array with the target variable, in this case the Sale Price. We start by setting the X and y variables, split into train and test sets using the train_test_split function from scikit-learn and initialize the LinearRegression estimator:
from sklearn.model_selection import train_test_split
# Set input features and output variable
y = all_data['SalePrice']
X = all_data.drop(['SalePrice'], axis =1)
# Split data into test and train sets
X_train, X_test, y_train, y_test = train_test_split(X, y.to_numpy().ravel(), test_size=0.30, random_state=101)
# OLS (and many other variants of regression) is housed in the linear_model module
from sklearn.linear_model import LinearRegression
# initialize the model
lr_model = LinearRegression()
The LinearRegression estimator, unlike many others, has very few configurable parameters. Above, we initialize it with all of the default values by passing no arguments to the function. Now we're ready to fit some data! We can do that by calling the .fit() method. This will be true for every Estimator in scikit-learn. We will use our training sub-datasets we created:
# Fit the model
lr_model.fit(X_train, y_train);
# The sklearn convention is to denote fitted parameters with a trailing underscore
print('Model y intercept:',lr_model.intercept_,'\n')
print('Model feature coefficients:',lr_model.coef_,'\n')
Model y intercept: -1348228.3926262031
Model feature coefficients: [-8.75772924e+01 5.95600326e+01 1.18930737e+00 1.38647884e+04
4.91899261e+03 4.10628404e+02 1.81486446e+02 1.51819223e+01
2.69056767e+01 -1.07411164e+00 -3.69107465e-01 2.54624576e+01
1.84098928e+01 2.14677482e+01 7.35941390e+00 4.72370548e+01
-8.14206679e+02 -6.09318362e+03 -1.52754837e+03 -1.82409326e+03
-1.58292462e+04 -2.59304669e+04 5.44696494e+03 -4.36801780e+01
-4.51893373e+01 4.11495671e+03 2.38219900e+01 4.82163185e+00
2.38325092e+01 3.04386635e+01 9.87034508e+00 4.14229568e+01
1.26489368e+02 -2.30107736e+00 2.62862323e+02 1.01150684e+02]
We can use these parameter estimates (y intercept and coefficients) to manually construct and apply a prediction equation (i.e.,
coeff_df = pd.DataFrame(lr_model.coef_,X.columns,columns=['Coefficient'])
coeff_df.head()
| Coefficient | |
| MSSubClass | -87.577292 |
| LotFrontage | 59.560033 |
| LotArea | 1.189307 |
| OverallQual | 13864.788358 |
| OverallCond | 4918.992610 |
Interpreting the coefficients:
- Holding all other features fixed, a 1 unit increase in Lot Frontage is associated with an **increase of $59.56 **.
- Holding all other features fixed, a 1 unit increase in Lot Area is associated with an **increase of $1.18 **.
- Holding all other features fixed, a 1 unit increase in Overall Condition is associated with an **increase of $4918.99 **.
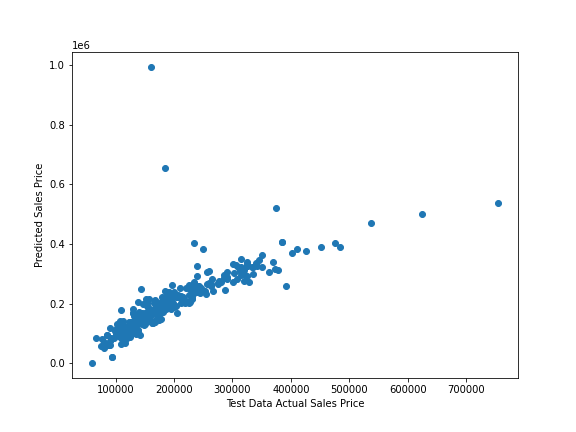
The next step is to use the trained model to predict new house Sale Price on new data. We do this by making use of the .predict() method that all Estimator classes implement. For example, here are the predicted scores for our X test data:
lr_predictions = lr_model.predict(X_test)
plt.scatter(y_test,lr_predictions);
plt.xlabel('Test Data Actual Sales Price');
plt.ylabel('Predicted Sales Price');
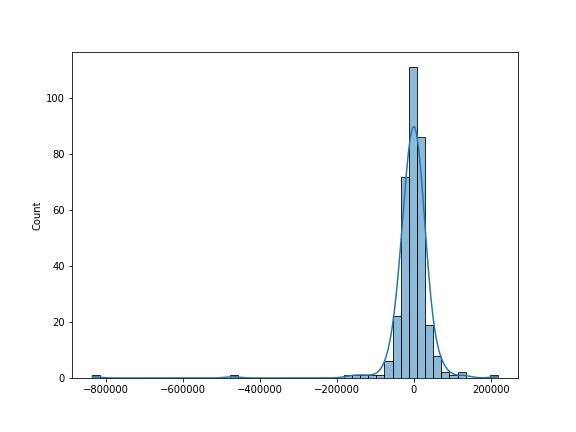
We can also plot the residual:
sns.histplot((y_test-lr_predictions),bins=50,kde=True);
Just to underscore how little we had to do, here's the whole example again, in three lines:
# Initialize the linear regression estimator
lr_model = LinearRegression()
# Fit the model
lr_model.fit(X_train, y_train)
# Generate predictions
lr_predictions = lr_model.predict(X_test)
Performance metrics¶
Once we've fit our model, it's natural to want to know how well it performs. In machine learning, the focus of model performance is on prediction; typically, we have some objective quantitative metric we care about, and to the degree that a model can produce better values on that metric, we incline to evaluate it more favorably. This doesn't mean that we have to single-mindedly base our evaluation of model on just one quantity; in practice, many other considerations may come into play (e.g., computational efficiency, interpretability, etc.). The point is mainly that machine learning practitioners—at least in applied settings—tend to care much more than traditional scientists do about what models can actually do, and much less about what's going on inside them.
The coefficient of determination¶
For the rest of this tutorial, we're going to focus our attention on one particular metric of predictive performance: the coefficient of determination, or
R-squared (R2) is the measure used to determine which line minimizes this distance:
Here are three other common evaluation metrics for machine learning problems:
- Mean Absolute Error (MAE) is the mean of the absolute value of the errors:
- Mean Squared Error (MSE) is the mean of the squared errors:
- Root Mean Squared Error (RMSE) is the square root of the mean of the squared errors:
Comparing these metrics:
- MAE is the easiest to understand, because it's the average error.
- MSE is more popular than MAE, because MSE "punishes" larger errors, which tends to be useful in the real world.
- RMSE is even more popular than MSE, because RMSE is interpretable in the "y" units.
All of these are loss functions, because we want to minimize them.
How well did we do?¶
Let's see how well the linear regression model we fitted earlier (using the house features as predictors) explains the variance in sales price. We'll make use of scikit-learn's metrics module, which contains a large number of predefined performance metrics. As is true of Estimator objects, all metrics in scikit-learn follow the same usage pattern: we pass in the true scores and the model's predicted scores, respectively.
# the metrics module contains predefined scoring functions
# for commonly used metrics like r^2, MSE, etc.
from sklearn import metrics
# scoring functions are called by passing an array of
# true scores and and an array of predicted scores as
# inputs
print('Model score:', metrics.r2_score(y_test, lr_predictions))
print('MAE:', metrics.mean_absolute_error(y_test, lr_predictions))
print('MSE:', metrics.mean_squared_error(y_test, lr_predictions))
print('RMSE:', np.sqrt(metrics.mean_squared_error(y_test, lr_predictions)))
Model score: 0.5238801531365112
MAE: 26110.712069211004
MSE: 3851956330.37256
RMSE: 62064.130787215254
Looking at the
For convenience, scikit-learn estimators have a .score() method you can use as an alternative to the above. Instead of generating predicted scores and then explicitly feeding them to a metric function like r2_score, you can call .score() directly on the estimator after the fit() step, and the prediction will be done implicitly:
# Initialize the estimator and fit the data, just like before
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)
# Now instead of generating predictions explicitly,
# we just call .score(). Note that we lose the ability to
# specify the metric: LinearRegression.score() always uses
# the R^2 metric.
lr_model.score(X_test, y_test)
0.5238801531365112
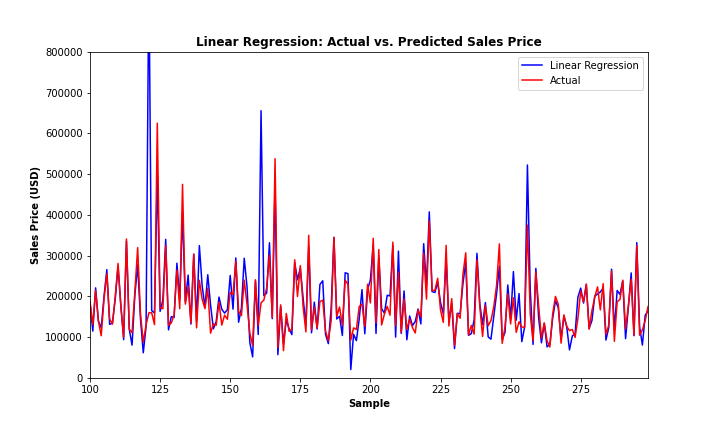
We can also look at how well we did visually by plotting the predicted vs. actual sales price values:
range_plot = range(100,300)
fig, ax = plt.subplots(figsize=(10,6))
lr_1 = ax.plot(range_plot, lr_predictions[range_plot], color='blue', label='Linear Regression')
lr_2 = ax.plot(range_plot, y_test[range_plot], color='red', label = 'Actual')
ax.set_ylim(0, 800000)
ax.set_xlim(range_plot[0], range_plot[-1])
plt.title('Linear Regression: Actual vs. Predicted Sales Price', fontweight='bold')
plt.xlabel('Sample', fontweight='bold')
plt.ylabel('Sales Price (USD)', fontweight='bold')
plt.legend(handles=[lr_1[0],lr_2[0]])
plt.show()